作者:張美虹/ 有勁生物科技
群集分析( cluster analysis )主要目的是將一大筆資料精簡成少數幾個同質性次群體( homogeneous subgroups ),以便從雜亂無章的一大堆原始資料中,做到分類、分群的目標。
群集分析法應用於高維度資料的分群,是多變量分析中常見的分析方法,可在廣泛的生物基因組數據中有效歸類出群集的相似性。舉例來說,對包含未知基因的群集進行分析,群集分析結果被歸類為同一群的基因都有類似的基因表現,由此推測被歸類到同類群集中的未知基因與已知基因應該具有相似的生物功能。
聚合式階層分群法(agglomerative hierarchical clustering)屬階層式分群法(hierarchical clustering)的一種,是群集分析中常見的應用。聚合式階層分群法是透過架構階層,將資料中相似的物件一層層一階階地反覆聚合分類,最後產生樹狀分支結構。此類分群法已被廣泛應用在醫學、自然科學及基因體學的資料分析上,希望藉由分析的結果去探究資料中的群集各有哪些特性或現象。
在階層式分群中,決定兩筆資料是否相似,是透過計算資料之間的「距離」遠近得知。而兩個群集之間的距離矩陣的計算有數種演算法,常見的有:
- 單一連結聚合演算法(single-linkage agglomerative algorithm):
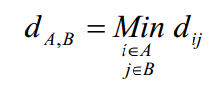
- 完整連結聚合演算法(complete-linkage agglomerative algorithm):

- 平均連結聚合演算法(average-linkage agglomerative algorithm):

- 中心聚合演算法 ( centroid method ) :

- 沃德法(Ward's method):

這些群集分類的演算方法,都是根據上述公式計算出的資料間相似性或測量距離,來分辨出同質性較高的少數群體,達到精簡資料的目的。這裡以沃德法稍作說明:該分群方式是先將每一個體視為單一群體,然後將各群體依序合併,合併的順序完全視合併後群體集合內的總變異數大小來決定。能使群集內總變異數產生最小增量的個體將優先合併,愈早合併的個體表示之間的相似性愈高。故沃德法又稱最小變異數法(minimum variance method) [1]。
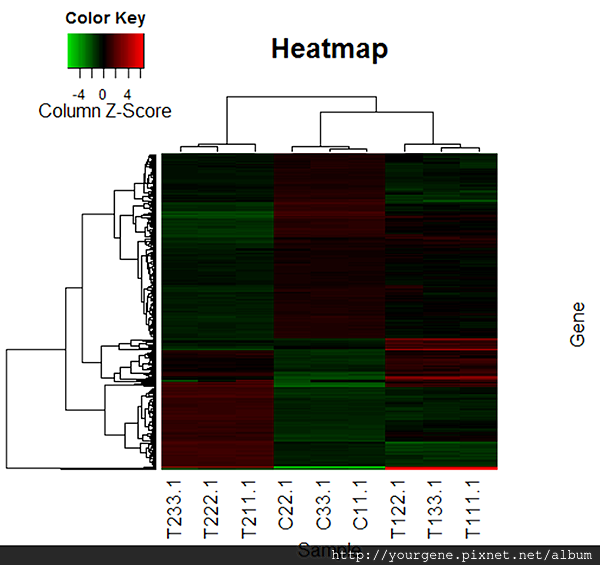
。熱圖在分子生物學上常用來視覺化叢集分析的結果,給予資料數據的矩陣值不同顏色,讓不同樣本間基因表現量的呈現或差異變得一目瞭然。然而,為了最佳化熱圖的視覺效果,我們常會針對資料矩陣進行微調。例如,將數值取對數成具正負值的型態以利區別基因表現量在不同樣品間所呈現的正相關或負相關;或者對數據進行標準化、或顯示數據的對應基因名稱等等。熱圖示意圖如下。[2]在R語言的環境中,可使用套件將群集分析的距離演算法計算所得以熱圖 (Heat map) 方式呈現
參考文獻:
1. Szekely, G. & Rizzo, M. (2005) Hierarchical Clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method. Journal of Classification. 22(2): 151-183.
2. Wilkinson L, Friendly M (2009) The history of the cluster heat map. The American Statistician. 63(2):179-184.





 留言列表
留言列表 {{ article.title }}
{{ article.title }}
